Um sehr kurze Lichtimpulse zu erzeugen werden modengekoppelte Laser verwendet. Die damit erzeugten Impulse können kürzer als eine Pikosekunde werden. Nach der Länge der Impulse heißen solche Laser Femtosekunden-Laser. Weil es aber nicht möglich ist, Laser für so kurze Impulse zu schalten, muss das Verfahren der Modenkopplung angewandt werden. Dabei werden verschiedene Moden eines Laserresonators zur gemeinsamen Schwingung angeregt.
Das folgende Bild zweigt drei verschiedene Moden eines Resonators mit jeweils zwanzig (rote Linie), einzundzwanzig (grüne Linie) und zweiundzwanzig Halbwellen (blaue Linie) zu einem Zeitpunkt.
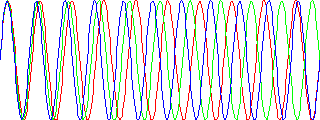
Die Kurven stellen dabei die elektrische Feldstärke an den Positionen des Resonators dar. Nach links ist die Position aufgetragen, nach oben und unten die Stärke des elektrischen Feldes. Man sieht nun, dass alle Kurven am linken Rand übereinander liegen, wärend die grüne Linie am rechten Rand den beiden anderen Linen entgegensteht. Nun kann man die Gesamtfeldstärke dieser drei Moden einfach durch Addition der Einzelmoden bestimmen. Das nennt man Superpositionsprinzip. Diese Summe ist im folgenden Bild dargestellt:
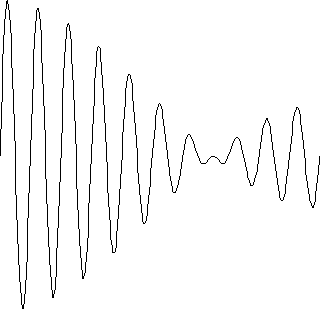
Die Feldstärke ist am linken Rand (wo sich die Einzelkurven überlappen) maximal und wird nach rechts kleiner.
Die drei Moden im Laserresonator schwingen aber nicht gleich schnell. Je kürzer die Wellenlänge einer Mode ist, desto schneller schwingt ihre Feldstärke auf und ab. Das folgende Bild zeigt die Moden nachdem die rote Mode genau eine Schwingung (auf und ab) vollzogen hat:
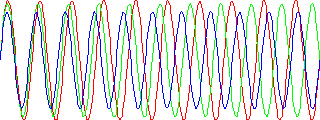
Hier erkannt man, dass die grüne und die blaue Kurve bereits etwas weiter geschwungen sind (sie sind beide über ihr Maximum hinaus). Noch etwas später, wenn die rote Mode fünf Schwingungen vollzogen hat, ergibt sich das folgende Bild:
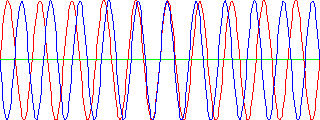
Die grüne Mode hat nun 5,25 Schwingungen vollzogen und ist gerade in ihrem Nulldurchgang, das heißt ihre elektrische Feldstärke ist überall Null. Die blaue Mode hat schon 5,5 Schwingungen vollzogen und nimmt damit das entgegengesetzte Maximum ein. Die Feldstärke zeigt in entgegengesetzter Richtung. Hier überlagern sich die Moden in der Mitte positiv, wärend sie einander an beiden Rändern entgegenstehen. Die Summe ist im folgenden Bild gezeigt:
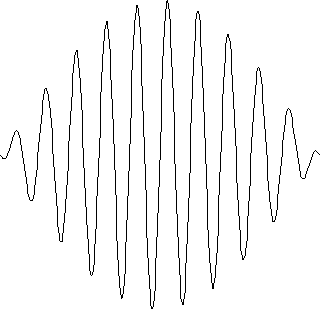
Das Maximum der gesamten Feldverteilung ist nun in die Mitte gewandert und man erkennt eine Art Wellenpaket im Zentrum des Resonators.
Weitere fünf Schwingungen weiter hat die rote Mode 10 Schwingungen, die grüne Mode 10,5 Schwingungen und die blaue Mode 11 Schwingen vollzogen. Es ergibt sich das folgende Bild:
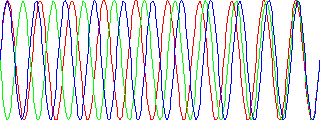
Alle Moden überlappen sich am rechten Rand. Die Spitze des Wellenpaketes sollte sich also bis zum Rand fortbewegt haben.
Nachdem ich die Überlagerung dreier Moden Schritt für Schritt erklärt habe, möchte ich nun das dynamische Verhalten von sechs Moden zeigen. Das folgende Bild zeigt also ein Wellenpaket, wie es entsteht, wenn man sechs Moden eines Resonators gemeinsam schwingen lässt. Der Übersichtlichkeit wegen ist nur die Summe dargestellt.
Dies ist das mathematische Modell für einen modengekoppelten Schwingungszustand in einem Laserresonator. In diesem modengekoppelten Zustand schwingt ein einzelnes Wellenpaket in dem Laserresonator hin und her. Das Wellenpaket ist um so schmaler, je mehr Moden beteiligt sind. Am Ausgangsspiegel kann ein Teil des Wellenpaketes ausgekoppelt werden und erzeugt einen periodisch wiederkehrenden kurzen Lichtblitz.
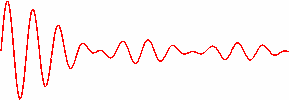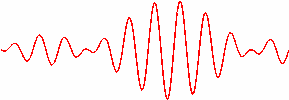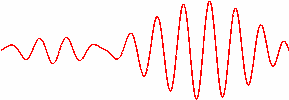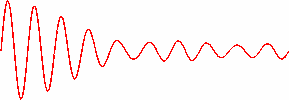
Das Beispiel von sechs gekoppelten Moden mit nur 20 Halbwellen ist nicht realistisch. Bei einer typischen Wellenlänge von weniger als einem Mikrometer wäre solch ein Laserresonator nur 1/100 Millimeter lang. Realistischer wäre schon ein zentimeterlanger Resonator mit 20000 Halbwellen. Hundert solcher Moden mit 20000 bis 20100 Halbwellen habe ich im folgenden Standbild zusammengekoppelt:

Man erkennt, dass bei vielen gekoppelten Moden ein relativ kurzer Lichtblitz mit langen beinahe feldfreien Zwischenräumen entsteht. In dem Laserresonator läuft also ein Wellenpaket hin und her und wird als kurzer Impuls ausgekoppelt. Der Resonator wird dabei zeitlich nicht verändert. Man erhält eine blinkende Lichtquelle in einem statischen Aufbau.
Ein realer Femtosekunden-Laser kann zu Beispiel eine Resonatorlänge von 30 Zentimeter haben. Da der Impuls mit Lichtgeschwindigkeit unterwegs ist, gibt das einen zeitlichen Abstand von 10 Nanosekunden. Die einzelnen Impulse sind im Femtosekundenbereich, also noch millionenmal kürzer. Dazu werden deutlich mehr Moden zusammengekoppelt.
©1999-2025 Joachim Schulz - Nur echt auf www.Quantenwelt.de
Letzte Änderung: 09.03.2012