Auf dieser Seite möchte ich die mathematische Formel der Schrödingergleichung erklären. Die Seite ist also eine Ergänzung zu meiner allgemeinverständlichen Erklärung ohne Formeln.
In ihrer einfachsten Form lautet die Schrödingergleichung:
Das ist die zeitunabhängige Schrödingergleichung.
In dieser Formel steckt mehr, als man ihr ansieht. Bei H handelt es sich nämlich nicht einfach eine Variable, sondern einen Operator. Ein Operator ist eine Rechenvorschrift, die auf eine ganze Funktion angewandt wird und diese in eine andere Funktion überführt. Ψ (sprich Psi) ist also auch nicht einfach eine Zahl, sondern eine Funktion, die von den drei Raumkoordinaten (wir nennen sie mal x, y und z) und der Zeitkoordinate (t) abhängt.
Die Unbekannte der Schrödingergleichung ist immer die Wellenfunktion Ψ. Der Operator H ist dagegen bekannt. E bezeichnet einen Energie-Eigenwert des Operators H bezüglich der Funktion Ψ. H heißt Hamilton-Operator und hängt vom untersuchten System ab. Er ist für ein Elektron im Atom anders als zum Beispiel für ein Silberatom in einem Magnetfeld. Der Hamiltonoperator beschreibt also die Art des Teilchens und der Felder, in denen es sich bewegt.
Man kann die zeitunabhängige Schrödingergleichung also als Frage nach derjenigen Wellenfunktion auffassen, auf die das Anwenden des Hamilton-Operators dieselbe Wirkung hat, als würde man die Wellenfunktion lediglich mit dem Energiewert E multiplizieren. In der Regel gibt es viele Lösungen der Schrödingergleichung und man muss zusätzliche Anfangsbedingungen vorgeben um eine spezielle Lösung zu erhalten.
Die obige Formel gibt den Hamilton-Operator in seiner allgemeinen Form an. Er besteht aus zwei Teilen, deren zweiter, V, nicht näher angegeben ist, weil er stark vom quantenmechanischen System abhängt. V ist die potenzielle Energie, gibt also alle beteiligten Kräfte und Felder an.
Der erste Teil des Operators errechnet dagegen die
Bewegungsenergie.
Hier taucht die Naturkonstante
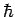(h quer) auf, die mit
dem planckschen Wirkungsquantum verbunden ist und für
quantenmechanische Rechnungen typisch ist.
Außerdem spielt die Masse eine Rolle, die
auch für die klassische kinetische Energie
(E=½mv²) wichtig ist.
Das Symbol ∇ heißt Nabla und bezeichnet eine Ableitung nach allen
Raumkoordinaten. Es wird eine doppelte Ableitung gebildet, die kinetische
Energie ist also von der Krümmung der Wellenfunktion abhängig.
Wellenfunktionen sind keine statischen Gebilde. Sie haben eine Zeitstruktur. Möchte man diese Zeitstruktur mathematisch untersuchen, sol muss man den Energie-Eigenwert durch einen Operator ersetzen:
Dieser Operator enthält eine
Ableitung nach der Zeit, vom Ort ist er nicht abhängig. Er enthält
ebenfalls die Konstante ,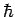
außerdem enthält er die imaginäre Konstante i, die Wurzel aus -1. Wellenfunktionen
müssen also durch komplexe Zahlen dargestellt werden, sie haben zwei
Komponenten, den Realteil und den Imaginärteil.
Ein wichtiges Zwischenergebnis ist, dass im Energieoperator nur eine Zeitabhängigkeit vorhanden ist, der Hamiltonoperator dagegen nur Ortsableitungen enthält. Wenn also in dem Potenzial V keine Zeitabhängigkeit vorhanden ist, können die beiden Seiten der Gleichung unabhängig gelöst werden. (Dies hängt damit zusammen, dass in zeitsymmetrischen Systemen Energieerhaltung gilt.)
Die Lösung dieses Operators und damit der zeitlichen Struktur
ist dann einfach. Funktionen, deren Zeitableitung ein imaginäres
Selbstabbild ist, sind einfache Kosinus- oder Sinusschwingungen.
Die Frequenz dieser Schwingungen ist gerade die Gesamtenergie
geteilt durch .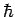
Wellenfunktionen schwingen also um so schneller, je größer ihr
Energiegehalt ist. Der linke Teil der Gleichung kann dann mit der
obigen zeitunabhängige Schrödingergleichung behandelt werden.
Hier habe ich die zeitunabhängige Schrödingergleichung nochmal ausgeschrieben. Das E auf der rechten Seite ist einfach eine Zahl, die die Gesamtenergie der Lösung angibt und Orts- und Zeitunabhängig ist.
Lösungen der zeitunabhängigen Schrödingergleichung zu finden ist fast nie einfach. Ich möchte hier auch nicht im Detail darauf eingehen. Für ein Elektron in der Umgebung eines Atomkerns ergeben sich als Lösungen die Atomorbitale.
Dass die zeitunabhängige Schrödingergleichung keine Zeitabhängigkeit besitzt, bedeutet nicht, dass man nur statische Probleme lösen kann. Die Zeitabhängigkeit der Lösungen wird hier nämlich nicht ignoriert, sie ist einfach bekannt (siehe oben). Man kann zeitabhängige Probleme lösen, indem man Lösungen verschiedener Energie miteinander mischt. Mit den statischen Orbitalen kann man zum Beispiel auch die Bewegung eines Elektrons als Wellenpaket um den Kern berechnen (Siehe Rydbergatome). Hierzu benutzt man das Verfahren der Überlagerung von Wellen.
Die ausgeschriebene zeitabhängige Schrödingergleichung lautet:
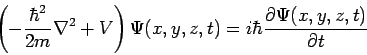
Man muss diese Gleichung nur in einem Schritt lösen, wenn die wirkenden Kräfte direkt von der Zeit abhängen. Sonst kann man jedes Problem mit der einfacheren zeitunabhängigen Schrödingergleichung lösen.
©1999-2022 Joachim Schulz - Nur echt auf www.Quantenwelt.de
Letzte Änderung: 30.05.2012